Tomas Miguel Rodriguez joined Kenyon College in 2024 after completing his Ph.D. from the University of Toledo. His research interests are in the field of operator theory in several complex variables. During the summer, he teaches mathematics to middle school students.
Areas of Expertise
Operator theory; several complex variables
Education
2024 — Doctor of Philosophy from University of Toledo
2018 — Master of Science from Indiana Univ-Purdue Indianapol
Courses Recently Taught
The first course in the calculus sequence, this course covers the basic ideas of differential calculus. Differential calculus is concerned primarily with the fundamental problem of determining instantaneous rates of change. In this course, we study instantaneous rates of change from both a qualitative geometric and a quantitative analytic perspective. We cover in detail the underlying theory, techniques and applications of the derivative. Elementary differential equations and their applications are also introduced, along with the basics of anti-differentiation. Students who have 4 credit hours for calculus may not receive credit for MATH 111. This counts toward the core course requirement for the major. Prerequisite: solid grounding in algebra, trigonometry and elementary functions. Offered every semester.
This is the second course calculus sequence, this course focuses on integration, including Riemann sums, the Fundamental Theorem of Calculus, techniques of integration, numerical methods, and applications of integration. This study leads into the analysis of differential equations by separation of variables, Euler's method, and slope fields. This counts toward the core course requirement for the major. Prerequisite: MATH 111 or the equivalent. Offered every semester.
The course starts with an introduction to the complex numbers and the complex plane. Next, students are asked to consider what it might mean to say that a complex function is differentiable (or analytic, as it is called in this context). For a complex function that takes a complex number z to f(z), it is easy to write down (and make sense of) the statement that f is analytic at z if \n\n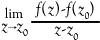
\n\nexists. Subsequently, we study the amazing results that come from making such a seemingly innocent assumption. Differentiability for functions of one complex variable turns out to be very different from differentiability in functions of one real variable. Topics covered include analyticity and the Cauchy-Riemann equations, complex integration, Cauchy's Theorem and its consequences, connections to power series, and the Residue Theorem and its applications. This counts toward the continuous/analytic (column B) elective requirement for the major. Prerequisite: MATH 224. Offered every other year.
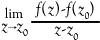\n\nexists. Subsequently, we study the amazing results that come from making such a seemingly innocent assumption. Differentiability for functions of one complex variable turns out to be very different from differentiability in functions of one real variable. Topics covered include analyticity and the Cauchy-Riemann equations, complex integration, Cauchy's Theorem and its consequences, connections to power series, and the Residue Theorem and its applications. This counts toward the continuous/analytic (column B) elective requirement for the major. Prerequisite: MATH 224. Offered every other year.