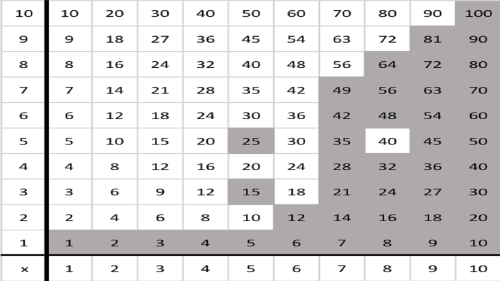
Can an asymptotically slower algorithm beat a naive and asymptotically faster algorithm in a record-setting computation? We show how this was done. We will look at three computational problems themed around elementary arithmetic to see how problems from antiquity continue to pose interesting challenges to modern computer science. The third problem will involve multiplication tables, the same table that every elementary school student is required to learn. We will evaluate M(n), the function that counts the distinct numbers in an n ✕ n multiplication table. The 10 ✕ 10 table has 42 distinct numbers in it; M(10) = 42. We modify an algorithm from antiquity, the sieve of Eratosthenes, to compute M(2^{30} - 1) = 204505763483830092.
Join us on Monday, January 22, for this exciting presentation from Jonathan Webster, associate professor of mathematics and actuarial science at Butler University. The presentation will begin at 4:10pm in Hayes Hall 109. We hope to see you there!