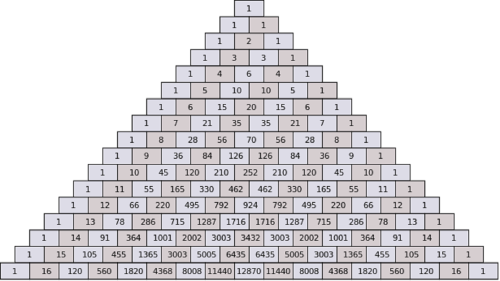
While Pascal's triangle is often taught within the context of elementary statistics, it holds great significance in subjects like combinatorics. In algebraic computation, Pascal's Triangle can be utilized to expand powers of binomials, but how exactly can an application like this generalize? We explore how triangles that generalize Pascal's hold secrets to efficiently computing everything from the betti numbers for projective hypersurfaces, to bounding the number points at which the partial derivatives of homogeneous polynomials can vanish in projective space.
Join us on Monday, Oct. 23, at 3:10 p.m. in Hayes 109 to hear this exciting presentation about Benjamin Castor's research. We hope to see you there!